わたしは
数学とか算数が小さいから苦手で高校生の時など数学の時間いっぱいを使って
「今日はどうやってあの娘を笑わかそうか・・」
というシナリオを作成するのに精いっぱいになってたほど数学が苦手です
そんな私が感心したお話があります
フェルマーの最終定理
知ってますか?
ふと見たドキュメンタリー番組でみて深掘りしてみたのだが
おもしろい

1670年に数学者のフェルマーが愛読してる算術の余白に書き込んである
メモがきっかけ死後息子が発見して発表
48項目あったうちの最後の一つ
300年誰も証明も反証もできなかった問いかけ
だからフェルマーの最終定理
胸があつくねぇすか
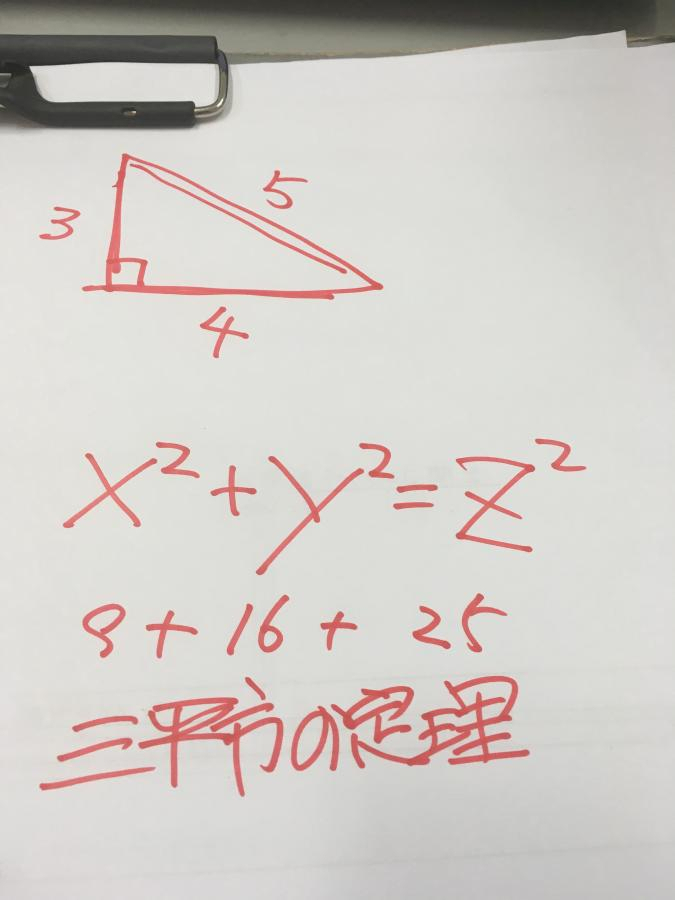
ちなみに
nを2にしたら上記はピタゴラスの定理
直角三角形の有名なヤツ
自分サッパリ意味わからんが
数式?が美しいそうです

日本では
さしご
基礎とか直角だすのにピタゴラスの定理つかってる
つかってた・・・・が現在ただしいのかな
300年間
当時の数学の大天才がやっとnを3にした時の証明ができた!!とか
少しずつ進んでた中
1955年
なんと!!にっぽん
志村、谷山予想ってのがでてきてー
(全然違う分野の二つの数式が似てるけど、もしかしてつながってるんじゃね?という予想)
完全に証明されてるものを定理 (ピタゴラスの定理とか)
証明されていないけど、おおむね合ってるんじゃね? が○○予想っていうらしい
なんやかんや
あってその谷山志村予想が証明されればフェルマーの定理が証明されるという仮説がたてられ
数々の天才数学者を地獄に落としてきた 悪魔の証明・・
人生を使って証明しようと試みるが結局証明できず「無駄な時間」をすごさせた・・・悪魔の証明が
1995年 アンドリュー ワイルズ が証明し330年もの歴史に決着がつきました
つい最近やん すごいすごい
このワイルズって人も結構あきらめそうになったり証明の発見のきっかけも
すっごいタイミングだったし
ふとしたひらめきだった
ドラマやね
まぁ
一番びっくりしたのは数学のすの字もわからない私がこの話をおもしろいと感じたこと
囲碁がサッパリわからんのにヒカルの碁が面白いのと一緒かな
興味のある方はフェルマーの最終定理で検索で
みなさん
こんにちは
がっつり解体やってます

ローカ床解体
階段のこし

全部床取っちゃうと階段落ちちゃうんで気をつかって解体

左図へ

UBを入れるとこの
サッシ新規なので済みだして解体中
うつくしく簡単な修繕になるよう計算しつくされた解体
誰も自分をほめてくれないので自分で自分をほめるのが
最近のマイブーム

!!!!
脱衣室の床をめくったら昔のトイレのタイルが出現
一番ガッカリするパターン

既存のタルキを利用して床組みをしたら
床が通気の関係でよろしくないのではと思い掘り下げを選択
こっちのほうが大工さん仕事しやすい
予定とうり作業が進む箇所もあれば予定とうり進まないところもあり
予定とうり進まない所は方向性を指示して道筋を照らしてあげればなんの問題もない
必要があればお客様と相談して道筋を見出していく
こうゆう創造性がリフォームのお仕事には割とあったりして柔軟性が必要とされるケースがある
こんなの苦手な人もいるとおもうけど
わたしゃこんなリフォームのお仕事が大好物です
オリバーリフォーム富山北
富山県富山市上赤江町1-1-45
お問い合わせ:050-1860-0236
ショールーム来店予約にてクオカードプレゼント!
お気軽にご来店ください☆
**************************************************
富山市・滑川市・黒部市・魚津市でリフォームをお考えなら、オリバーリフォームにおまかせください!
























